Review 2

I missed this because I didn't divide both sides by 1/2 then divide both sides by (b1+b2)

Vocabulary

Vocabulary Final Exam Folder | Quizlet

Section 1 

Section 2 

Section 3 

Section 4

Section 5 

Review 1

These are the questions I missed:

I missed this because I didn't round to the nearest meter

I missed this because I didn't find the smallest are

I missed this because i didn't find the smallest volume

Transformations

Transformations Game

Linear Programming

Vertices:	(0,6)		(0,0)		(6,0)
Constraints	Objective Function: C=3x+4y
x ≥ 0 y ≥ 0 x + y ≤ 5	C=24	C=0		C=18

Vertices	(-15,0)		(0,6)		(5,0)
Constraints	Objective Function: C= -2x+5y
x≤5 y≥4 -2x+5y≤30	C=30	C=30		C=-10

Vertices:	(1,8)		(1,2)		(5,2)
Constraints	Objective Function: C=7x+3y
x≥1 y≥2 6x+4y≤38	C=31	C=13		C= 42

Vertices:	(0,8)		(0,4)		(6,8)
Constraints	Objective Function: 4x+6y
y≥0 y≤8 -2x+3y≥12	C=48	C=24		C=72

Vertices:	(0,5)		(0,0)		(5,0)		(2,3)
Constraints	Objective Function: C=8x+7y
x ≥ 0 y ≥ 0 4x + 4y ≤ 20 x+2y ≤8	C=35	C=0		C=40		C=37

Vertices:	(0,2)		(3,0)		(4,3)		(0,4)
Constraints	Objective Function: C=3x+5y
x ≥ 0 2x+3y ≥ 6 3x - y ≤ 9 x+4y≤16	C=10	C=9		C=27		C=20

Statistics Test

Statistics Test 

Graphing Exponential Growth/ Decay

Formula : Y=a*b ^{x –h} +K

• Domain :  (-∞,∞) - All Real Numbers
• Range : y >k - a is positive 

                   y< k - a is negative 

• Asymptote : y=k
• H= left/right (opposite)
• K= up/ down 
• A= Multiplier 

           a >1 = stretch

           0<a<1 = compression

           a< 0 (negative) = flip over x axis 

• B= base 

           b>1 = Growth (always increasing)

          0<b<1 = Decay ( always decreasing) 

Statistics

Statistics Data 

Compound Interest Formula

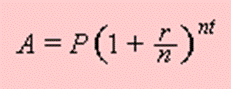
P: Principal , amount o money borrowed
R: Rate of interest ( written as a decimal
N: Number of times compounded
          Annually: 1
          Semiannually: 2
          Monthly: 12
          Quarterly : 4
T: Time (always in years)

Things to Remember : 

• There are 52 weeks in a year
• There are 365 days in a year
• There are 4 quarters in a year

Example: An amount of $1,500 is deposited in a bank paying an annual interest rate of 4.3%, compounded quarterly. What is the balance after 6 years?

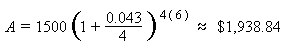
General Forms of a Sequence

• Sequence: a list of numbers
• Finite Sequence: a sequence that ends

              Example : 1,3,9,12 

• Infinite Sequence: a sequence that keeps going 

             Example: 1,3,9,12,15,18...

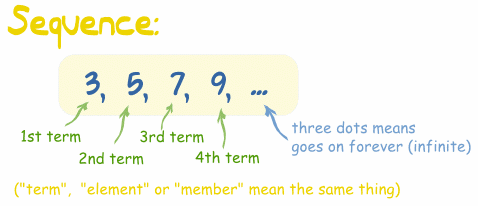
Types of Sequences 

• Arithmetic Sequence: have a common difference and you find it by subtracting the last number from the next and so on. 

                       Example:  1,4,7,10,13 

                       13-10 =3 

                       10-7=3

                        7-4=3

                        4-1=3                      

                                  So the common difference is 3 which is represented as d=3 

The formula that represents arithmetic sequences is:

             

• Geometric Sequences: have a common ration and you can find it by dividing the last number by the next number. 

                              Example : 4,24,144,864....

                          864/144=6

                          144/24=6

                           24/4=6

                                                  So the common ration is 6 represented as r=6

The formula that represents geometric sequences :

To find a specific term in a sequence you  just plug that number into the A_n

                                             

Characteristics & Traits

• Domain : x values, describes a graph as it moves from left to right.
• Range: y values, describe a graph as it goes up and down.
• End Behavior: describes what happens on both ends.  

                     Left:  

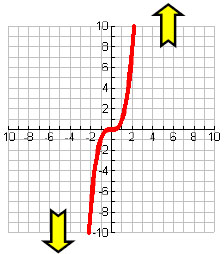
• Absolute Max/ Min: lowest/ highest point
• Local Max/Min: more than one highest or lowest point

• Interval of Increase: what happens to y values as you move along x axis.
• Interval of Decrease : describe what happens to the graph as you move left ans right on x axis.
• X Intercept: (a,0)
• Y Intercept : (0,b) 
•  
• Symmetry:           

1. Even: symmetric about the y axis
2. Odd:  rotational symmetry about origin
3. Neither: None   

• Asymptotes: imaginary line that a graph gets closer to, but never touches
• Function: passes vertical line test

 This picture does not pass vertical line test, so it is not a function

• One to One: passes horizontal line test